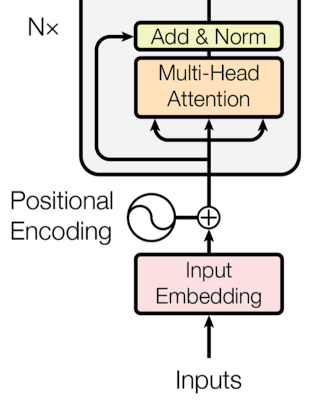
What is positional encoding?

Positional encoding was originally mentioned as a part of the Transformer architecture in the landmark paper “Attention is all you need” [Vaswani et al., 2017]. This concept is first introduced under the name of position embedding in [Gehring et al., 2017] where it was used in the context of sequence modelling with convolutional architectures.

In the Transformer architecture, positional encoding is used to give the order context to the non-recurrent architecture of multi-head attention. Let’s unpack that sentence a bit. When the recurrent networks are fed with sequence inputs, the sequential order (ordering of time-steps) is implicitly defined by the input. However, the Multi-Head Attention layer in the Transformer is a feed-forward layer and reads a whole sequence at once. As the attention is computed on each datapoint (time-step) independently, the context of ordering between datapoints is lost and the attention is invariant to the sequence order. The same is generally true for other non-recurrent architectures like convolutional layers where only a small sequential ordering context is present, limited by the size of the convolution kernel.

To alleviate this problem, the concept of positional encoding is used. This is nothing more than adding a tensor (of the same shape as the input sequence) with specific properties to the input sequence. The positional encoding tensor should be such that the value difference of the specific steps in the sequence correlates to the distance of individual steps in time (sequence).

What is Absolute Positional Encoding?

The simplest example of positional encoding is an ordered list of values, between 0 and 1, of a length equal to the input sequence length, which is then tiled to the same number of features as the network input and added to that input.

Authors of [Vaswani et al., 2017] however proposed a different absolute positional encoding based on the sine and cosine functions:

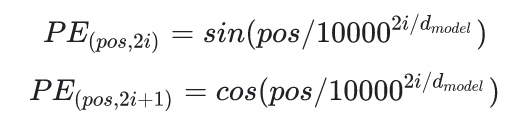
where pos is the position in time, dmodel is the number of dimensions and i is the dimension index in the input tensor. This way each wavelength is a geometric progression from 2π to 2kπ. To make this more clear here is a code snippet that plots this positional encoding table for an imaginary input tensor with 200 time steps and 12 channels:

import numpy as np
import seaborn as sns

def sinusoid_positional_encoding_ref(length, dimensions):  
    def get_position_angle_vec(position):
        return [position / np.power(10000, 2 * (i // 2) / dimensions) for i in range(dimensions)]

    PE = np.array([get_position_angle_vec(i) for i in range(length)])
    PE[:, 0::2] = np.sin(PE[:, 0::2])  # dim 2i
    PE[:, 1::2] = np.cos(PE[:, 1::2])  # dim 2i+1
    return PE

pe = sinusoid_positional_encoding_ref(200, 12)

sns.set(rc={'figure.figsize':(14,4)})
ax = sns.heatmap(pe.T)
ax.invert_yaxis()
ax.set_ylabel("input dimension")
ax.set_xlabel("time step")
ax.set_title("Sinusoid absolute positional encoding")

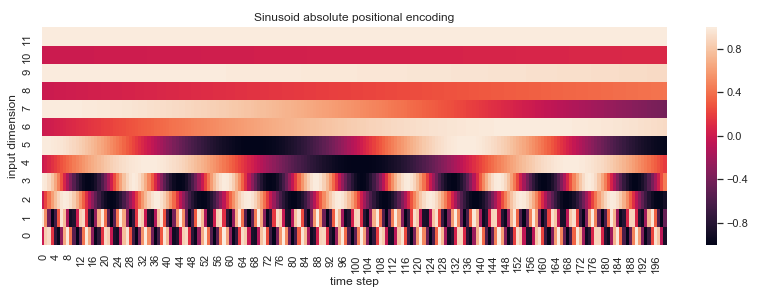
The authors hypothesize that this type of absolute positional encoding supports models in learning to attend to relative positions, as any fixed offset k, PEpos+k is representable as a linear function of PEpos.

But why not just use the one-hot encoding of position? Ideally, we want the attention mechanism to be able to generalize to the input sequences longer than the ones encountered in the training set. Using the one-hot position encoding, even if the dataset contained a uniform distribution of all input lengths that the model need to generalize to, the model would still be biased as it would learn the embedding of earlier positions much better because it would encounter them more often during training.

If we think about this problem, we may conclude that the same bias might occur even with the sinusoid-based absolute positional encoding. This led to a follow-up study [Shaw et al., 2018] where the issue of generalizing to arbitrary input lengths is tackled, and the relative positional encoding is introduced.

Another variant of absolute positional encoding exists where the position embeddings are learned jointly with the network model during training. This method suffered from the same generalization issues as the fixed absolute positional encoding methods.

What is Relative Positional Encoding?

The paper “Self-Attention with Relative Position Representations” [Shaw et al., 2018] introduces the concept of relative positional encoding. This concept incorporates the explicit representations of relative position in the self-attention mechanism which significantly improves the performance of the Transformer architecture.

Conceptually the relative positional encoding allows the self-attention to consider arbitrary relations between any two elements in the input. The authors of [Shaw et al., 2018] focused on the efficient implementation, and the change to the self-attention equations is minimal:

As we can see the only change is in the addition of the new vector to the products of key and value matrices with the input. This new vector is trained jointly with the model and is supposed to learn the additive component which is going to augment the previously mentioned product xW with the relative position context. To make it clearer let’s look at how this vector is built.

So the relative distance context this vector can represent is clipped to k in both directions. For example, if we have k=3, we learn only the relative position embeddings up to distance 3 between the tokens. When the distance between tokens is greater than 3, the embedding returns the same value as for distance equal to 3. Here is a visualisation of such an imaginary learned positional vector:

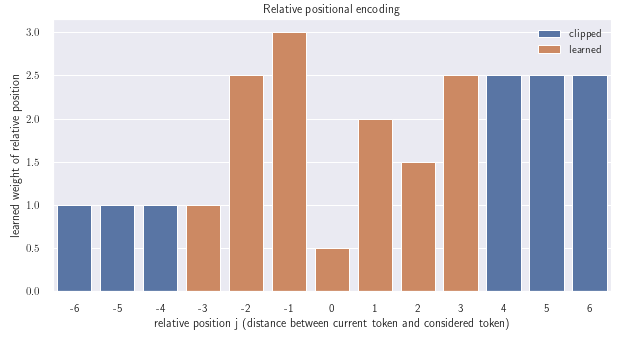
The main advantage of this method is that the positional embedding depends only on the relative distance between the tokens, and not on their absolute position in the sequence. This should lead to a more robust generalization of the attention beyond the sequence lengths present in the training set. This has been demonstrated in [Shaw et al., 2018] by achieving significantly better results than the models with absolute positional encoding. More methodical comparison of the two methods has been conducted in [Rosendahl et al., 2019] where it is again shown that the relative positional encoding is superior when translating sequences that are longer than any observed training sequence

What is RNN based positional encoding?

Since recurrent layers have implicit information about the order of input sequence, these have often been used as a layer preceding the Transformer or any other attention mechanism to endow the input sequence with the order context. This type of RNN+Attention architecture was usually trained jointly which often leads to the result where RNN is able to perform a lot of the computation required for solving the task and not only give the positional embedding to the input.

Transformers trained directly on the input sequences allow for easier interpretation, as the attention layers can be probed to reveal the learned relationships between elements in the input sequence. When an RNN is placed in front of the Transformer, the input gets convoluted which makes such interpretations impossible.

Positional encoding for tree-structured data

So far we discussed positional encoding use for processing sequential data with attention based architecture. However there is a growing interest in applying the attention methods on the tree-structured data and tasks like programming language analysis, language parse trees translation, and semantic parsing like extracting a database query from a natural language request.

The paper [Shiv and Quirk, 2019] introduces tree positional encoding using a stack-like encoding for tree positions. The authors demonstrate a significant increase in the performance of transformers using tree positional encodings for a multitude of tasks compared to the original sequence focused transformers.

How to do positional encoding for irregularly sampled data?

There are quite a few options for dealing with irregularly sampled data, or time-series data with non-equidistant timesteps. I discuss this in more details in a different post:

Corrupt, sparse, irregular and ugly: Deep learning on time series